Grundlagen

Das erste Bild

Beim Erstellen des ersten Bildes ist es gut, wenn man sich gedanklich in ein Fotostudio versetzt. So benötigt jedes Bild midestens drei Elemente, die auch dort vorkommen. Das ist die Kamera, mindestens eine Lichtquelle und ein Objekt, das betrachtet wird. Im ersten Bild ist dies eine Kugel, das einfachste Objekt bei "POV-Ray(TM)". Machen wir uns also frisch ans Werk:

        #version 3.6;
        
        camera{ location <0, 5, -20> look_at <0,0,0> } //Ort, Ausrichtung
        light_source{ <0, 15, -2> color rgb<1,1,1> } //Ort, Farbe
        sphere{ <0,0,0>,2 pigment{color rgb<1,1,1>} } //Mittelpunkt, Radius

        //Hinweis:
        // Zwei Schrägstriche kommentieren den Rest der Zeile aus
        /* Was zwischen diesen Zeichen steht ist auch auskommentiert */
        

Dabei stehen Werte in spitzen Klammern "<1,1,1>" für Vektoren, die im Kapitel Grundlagen Teil 2 beschrieben werden. Für die ersten Schrite ist dieses Wissen nicht erforderlich. Viel mehr wollen wir uns zunächst anschauen, wie das eben erstellte Bild aussieht und wie es zustande gekommen ist.

Um zu verstehen, wie es zu der weißen Kugel auf schwarzem Grund kommt, schauen wir uns die Befehle etwas genauer an. Zunächst wird die Position der Kamera bestimmt und der Punkt, auf den sie ausgerichtet ist. Dabei kann man sich das Ganze wie in einem Filmstudio vorstellen. Die Kamera steht an einer bestimmten Stelle im Studio und macht Bilder von der Szene.
Als nächstes kommt die Lichtquelle, die ebenfalls eine Position zugewiesen bekommt. Auch wenn die Lichtquelle unsichtbar ist, spielt ihre Position eine entscheidene Rolle. So generiert "POV-Ray(TM)" aus der Postion der Lichtquelle den Schattenwurf des Objekts. Daher ist die untere Seite der Kugel dunkel, da sie von der oberen Hälfte verdeckt wird. Probiert den Effekt ruhig ein wenig aus und verschiebt die Lichtquelle auf die Postion "<0,5,-5>" um zu sehen wie sich der Schatten verändert. Nach der Postion wird noch die Farbe der Lichtquelle definiert. Dabei steht rgb für rot/grün/blau, wobei "1" den Wert "255" (also maximale Intensität) bedeutet. Damit ergibt rgb<1,1,1> die Farbe weiß, da alle Grundfarben in maximaler Intensität vorkommen.
Zuletzt haben wir den dargestellen Gegenstand definiert. Dabei handelt es sich um eine Kugel, die im Ursprung ihren Mittelpunkt hat und den Radius 2 besitzt. Wie bei der Lichtquelle folgt am Schluß die Definition der Farbe. Dabei haben wir auch der Kugel die Farbe Weiß gegeben, damit sie sich vom schwarzen Hintergund abhebt. Wird in "POV-Ray(TM)" keine Farbe angegeben, so bleibt der Gegenstand schwarz. Allerdings ist zu beachten, dass einer Lichtquelle direkt eine Farbe zugewiesen werden kann, während bei Gegenständen die Angabe pigment "ankündigt", dass jetzt die gewünschte Farbe folgt.
Wir haben somit erfolgreich das erste Bild erstellt und dabei einige Grundlagen des Raytracers verstanden. Jetzt wird es Zeit ein wenig genauer auf das zu grunde liegende Koordinatensystem zu schauen, um zu verstehen wie man Objekte gezielt positionieren kann.

Jetzt wird's kantig

Neben der Kugel (sphere) zählen Quader (box), Zylinder (cylinder) und Kegel (cone) zu den grundlegenden geometrischen Formen. Daher wollten wir uns nun in genau dieser Reihenfolge damit befassen.
Ein Quader benötigt genau zwei Angaben: Die hintere, linke Ecke und die vordere, rechte Ecke. Das sieht als Beispiel dann wie folgt aus:

        box{ <-1,-2,-3>,<3,2,1> } //hinten links, vorne rechts
        

In diesem Fall liegt also die hintere, linke Ecke im Punkt <x=-1, y=-2, z=-3> und die vordere, rechte Ecke hat die Koordinaten <x=3, y=2, z=1> weshalb wir einen Würfel mit Kantelänge 4 Einheiten erhalten.

Um einen Zylinder zu erstellen braucht es insgesamt drei Angaben:

        cylinder{ <0,2,0>,<4,2,0>,2 } //Mitte 1.Kreis, Mitte 2.Kreis, Radius
        

Dabei gibt die erste Koordinate den Mittelpunkt des unteren (bzw. des ersten Kreises), während die zweite Angabe für den Mittelpunkt des oberen Kreises steht. Schließlich gibt der dritte Wert den Radius der Kreise an. Obige Zeile erstellt also einen Zylinder, dessen Mittelpunkt zwei Einheiten in y-Richtung verschoben ist und der sich über vier Einheiten entlang der x-Achse erstreckt. Der Radius beträgt zwei Einheiten. Übrigens gibt die zweite Koordinate (Mittelpunkt des oberen Kreises) an, wie der Zylinder ausgerichtet ist. In unserem Fall liegt er entlang der x-Achse. Er lässt sich aber auch einfach "aufstellen", indem wir die zweite Koordinate etwas abändern:

        cylinder{ <0,2,0>,<0,6,0>,2 }
        

In diesem Fall "steht" der Zylinder, er ist also entlang der y-Achse ausgerichtet. Da wir bisher immer nur eine Koordinate verändert haben, liegt der Zylinder immer entlang einer der Koordinaten-Achsen. Natülich lassen sich auch Zylinder erstellen die schräg im Koordinatensystem liegen. Dafür muss man einfach zwei oder drei Koordinaten ändern.

Zuletzt wollen wir uns hier noch den Kegel anschauen. Dieser braucht vier Angaben, um klar definiert zu sein. Zunächst gibt man die Position des unteren Mittelpunkts an, gefolgt vom Radius des unteren Kreises. Als nächstes wird wir der Mittelpunkt des oberen Kreises angegeben, sowie dessen Radius:

        cone{ <0,2,0>,2, <0,5,0>,0.5 }
        //Mitte Grundfläche, Radius Grundfläche, Mitte Spitze, Radius Spitze
        

Damit erstellen wir einen Kegelausschnitt, bei dem die Spitze abgeschnitten ist. Will man einen Kegel mit Spitze erstellen, so muss man sich einem Trick bedienen. Es ist nämlich nicht möglich den oberen Radius Null zu setzten oder gar einfach weg zu lassen. Das führt bei der Erstellung des Bilds zwangsläufig zu einem Fehler. Statt dessen kann der Radius aber sehr klein (nahe Null) gewählt werden, was im Bild dann zu einer geschlossenen Spitze führt:

        cone{ <0,2,0>,2, <0,5,0>,1.0e-4 }
        

Dabei steht 1.0e-4 für 10^-4 = 0,0001, was ausreicht um eine geschlossenen Spitze zu erstellen. Da es sich beim Kegel genau genommen um eine Sonderform des Zylinders handelt, gelten hier auch die selben Regeln bei der Erstellung. So wird auch beim Kegel die Ausrichtung über die Angabe des Mittelpunkts des oberen Kreises festgelegt. Ebenso lassen sich durch ändern mehrerer Koordinaten Kegel erstellen, die schräg im Koordinatensystem liegen.

Mit einem kleinen Bild wollen wir das eben gelernte veranschaulichen:

        #version 3.6;
        
        camera{ location <0, 5, -20> look_at <0,0,0> }
        light_source{ <0, 15, -2> color rgb<1,1,1> } 

        box{ <-6,0,6>,<-2,4,2> pigment{rgb<1,0,0>} }
        cylinder{ <0,0,-2>,<1,4,-1>,2 pigment{rgb<0,1,0>} }
        cone{ <4,0,-2>,2 <4,4,-2>,0.1 pigment{rgb<0,0,1>} }
        

Damit erzeugen wir ein Bild, mit einem roten Qader im Hintergund, einem grünen, schräg stehenden Zylinder sowie einem blauen Kegel im Vordergrund:

Mit ein wenig Phantasie lassen sich mit diesen grundlegenden Formen schon ganz nette Bilder erzeugen. Damit wir jedoch besser verstehen, was wir tun, wollen wir uns im nächsten Kapitel das Koordinatensystem und Transformationen anschauen.

Verschiebungen im Koordinatensystem

Um beim Raytracing gezielt Objekte platzieren zu können, muss das Koordinatensystem verstanden sein. Daher widmet sich dieses Kapitel zunächst den Vektoren. Anschließend wird erklärt, wie Objekte mit translate, rotate und scale manipuliert werden können.

Das Koordinatensystem

Beim Raytracing werden alle Gegenstände in einem echten 3D-Koordinatensystem erstellt. Daher benötigt jeder Punkt (z.B. der Mittelpunkt einer Kugel) die Angabe von drei Koordinaten. Die Eingabe erfolgt über die im vorherigen Abschnitt eingeführte Schreibweise mit Hilfe von spitzen Klammern. Dabei gibt der erste Wert an, wie weit der Gegenstand nach rechts bzw. links vorschoben wird (x-Koordinate), an zweiter Stelle steht die Höhe des Gegenstands (y-Koordinate), wobei die dritte Zahl angibt, wie weit vorne oder hinten ein Gegenstand platziert wird (z-Koordinate). Grafisch dargestellt ergibt sich dabei folgendes Bild:

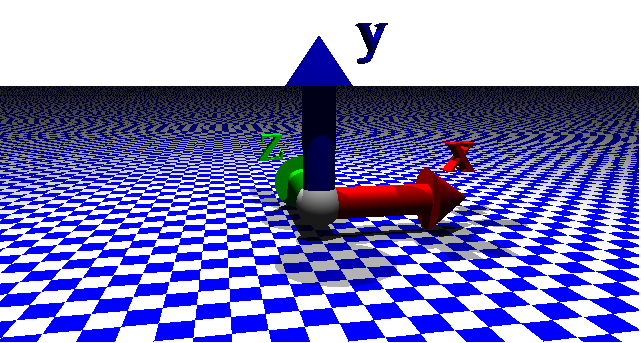
Das Koordinatensystem wurde dabei leicht gedreht, um alle Pfeile besser sichtbar zu machen.
Der rote Pfeil zeigt dabei in positive x-Richtung, Blau gibt die positive y-Richtung an, während vom grünen Pfeil die positive z-Richtung markiert wird. Kurzgefasst sieht ein Vektor also wie folgt aus:

Wollen wir den Mittelpunkt der Kugel also nicht im Ursprung sitzen haben, sondern zwei Einheiten nach oben und eine Einheite nach links verschoben, so müssem wir folgendes eingeben:

        sphere{ <-1,2,0>,2 pigment{color rgb<1,1,1>} }
        

In aufwendigen Bilder ist es oft hilfreich die Gegenstände im Ursprung zu erstellen und dann an die gewünschte Postion zu verschieben. Damit lassen sie sich einfacher relativ zueinander ausrichten. Dafür gibt es die Operation translate. Die verschobene Kugel könnte man also auch folgendermaßen erstellen:

        sphere{ <0,0,0>,2 pigment{color rgb<1,1,1>} translate<-1,2,0> }
        

Die Kugel wird in diesem Fall im Ursprung erstellt und anschließend an die gewünschte Stelle verschoben. Will man einen Gegenstand nur in eine der Koordinaten-Richtungen verschieben, so kann man sich einer einfacheren Schreibweise bedienen:

        sphere{ <0,0,0>,2 pigment{color rgb<1,1,1>} translate 2*y }
        

Damit verschieben wir die Kugel lediglich um 2 Einheiten nach oben. Der Vorteil dieser Methode zeigt sich allerdings nur bei sehr aufwendigen Bildern, da sie ein klein bischen weniger Rechnenleistung benötigt, als die erste Möglichkeit.
Das Verschieben von Gegenständen lohnt sich jedoch nur, wenn auch mehrere Objekte auf dem Bild zu sehen sind. Dabei kann "POV-Ray(TM)" wesentlich mehr als nur Kugeln erstellen. Die einfachsten dieser Formen werden im folgenden Abschnitt erklärt.

Transformationen

Gegenstände lassen sich nicht nur verschieben, viel mehr gibt es noch zwei andere fundamentale Operationen um sie zu manipulieren. So lässt sich zum einen die Größe ändern (skalieren) und zum anderen kann man sie drehen.
Die Größe ändert man dabei durch die Opertation scale:

        #version 3.6;
        
        camera{ location <0, 5, -20> look_at <0,0,0> } 
        light_source{ <0, 0, -10> color rgb<1,1,1> } 

        sphere{ <0,0,0>,2 pigment{color rgb<1,1,0>} }
        sphere{ <0,3,0>,1 pigment{color rgb<0,1,1> scale 2} }
        

Mit der Operation scale 2 wird die Kugel in allen Raumrichtungen verdoppelt. So kann man in obigem Bild gut sehen, dass beide Kugeln gleich groß sind. Wie bei der Verschiebung könnte man sich daher fragen, wozu scale überhaupt gut ist. Dies lässt sich an einem zweiten Beispiel erklären:

        sphere{ <0,3,0>,1 pigment{color rgb<0,1,1>} scale<1,3,0.8> }
        

Die Operation scale lässt sich auch als Vektor angeben, wobei dann die jeweile Ausdehnung entsprechend verändert wird. So bleibt in diesem Beispiel die Ausdehnung in x-Richtung gleich, während die y-Richtung um Faktor drei gestreckt wird. Werte die kleiner als eins sind, verkleinern dagegen die Ausdehnung in diese Richtung. Daher wird die Ausdehnung in z-Richtung der Kugel in diesem Fall auf 4/5 verkleinert. Damit lassen sich sehr interessante Formen erstellen. Allerdings muss man beim Umgang mit dieser Operation gut aufpassen, denn:

"You know you have been raytracing too long when...
...You buy your furniture no matter of size cause you can scale it to fit into your room."
- Peter Christian -

Drehen lassen sich Gegenstände über die Operation rotate. Bei Kugeln hat dies aufgrund der Symmetrie zwar keinen Effekt, doch kennen wir mittlerweile noch weitere Formen. Wir bedienen uns daher dem bekannten Kegel, der aufrecht steht:

        #version 3.6;
        
        camera{ location <0, -6, -10> look_at <0,0,0> }
        light_source{ <0, 2, -10> color rgb<1,1,1> }

        cone{ <4,0,-2>,2 <4,4,-2>,0.1 pigment{rgb<0,0,1>} }
        

Diesen wollen wir nun so drehen, dass er entlang der x-Achse liegt und die Spitze nach links zeigt.

        #version 3.6;
        
        camera{ location <0, -6, -10> look_at <0,0,0> }
        light_source{ <0, 2, -10> color rgb<1,1,1> }

        cone{ <0,2,0>,2 <0,6,0>,0.1 rotate<0,0,-90> pigment{rgb<0,0,1>} }
        

Wie wir sehen hat die Operation den gewünschten Effekt erzielt. Doch wie kommt die Drehung zustande? Schauen wir uns dazu den Ausdruck rotate<0,0,-90> genauer an. Zunächst steht das rotate für die Operation, nämlich für eine Drehung. Gefolgt wird sie von einem Vektor mit drei Angaben. Dabei steht der erste Eintrag für den Winkel in x-Richtung. In unserem Fall wird die Figur um 0° (also gar nicht) um die x-Achse gedreht. Würden im ersten Eintrag 90° stehen, so würde der Kegel "nach hinten umfallen". Der zweite Eintrag gibt die Drehung um die y-Achse an, wobei der letzte Eintrag schließlich angibt, wie viel um die z-Achse gedreht wird.
Um den Vorgang der Drehung besser zu verstehen schauen wir uns in folgendem Bild an, was mit dem Kegel während der Drehung geschieht.

Dabei zeigt der grüne Pfeil in positive z-Richtung. Der gelbe Pfeil zeigt die positive Drehrichtung um die z-Achse (gegen den Uhrzeigersinn). Im ersten Bild ist der Kegel noch nicht gedreht, wobei das zweite Bild den Kegel um -30° um die z-Achse gedreht zeigt. Im letzten Bild wurde der Kegel schließlich um -60° gedreht. Gut zu sehen ist dabei, dass der Kegel im Uhrzeigersinn, also in negative Richtung gedreht wird, was wir aufgrund des Vorzeichens auch so erwartet haben.
Beim Drehen von Formen und Figuren ist ein wenig Erfahrung nötig, vor allem, wenn gleichzeitig um zwei Achsen gedreht wird. Hier heißt es: Nicht gleich verzweifeln, sondern einfach ein wenig ausporbieren.

Ein erstes Motiv aus einfachen Formen

In den letzten Kapiteln haben wir alle grundlegenden Formen und Transformationen kennen gelernt. Damit unsere Objekte jedoch nicht einfach im Raum schweben, fehlen noch zwei wichtige Dinge: plane erstellt eine Ebene, die als Boden dient und background füllt den Hintergund mit einer Farbe. Nachdem wir uns diese beiden Elemente in "POV-Ray(TM)" angeschaut haben, werden wir eine hübsche Bauklötzchen-Burg rendern.

Gestaltung des Hintergrunds

Zunächst wollen wir die Hintergundfarbe anpassen. Dies geht ganz einfach über die Angabe

        background{rgb<0,0,1>}
        

Schon wird der Hintergund in Blau angezeigt. Dabei sollte jedoch beachtet werden, dass der Hintergund wirklich nur eine Farbe besitzen kann. Daher braucht man kein pigment vor die Farbe zu setzen, da hier ja nur eine Farbe als Argument erlaubt ist. Will man jedoch weiße Wolken am Himmel haben, muss man diese als extra Objekte erstellen und dann einfügen. Schließlich darf der Hintergund nur eine Farbe besitzen, also entweder Weiß oder Blau, aber nicht beides vermischt.

Einen Untergund (z.B. eine Tischplatte) zu erstellen ist ein wenig schwieriger, da wir hierfür eine Ebene benötigen. Wer im Mathe-Unterricht aufgepasst hat, der weiß, dass es verschiedene Arten gibt eine Ebene zu beschreiben. "POV-Ray(TM)" geht hier den "bequemen" Weg über den Normalenvektor. Man gibt also den Normalenvektor der Ebene an, sowie an welcher Postion sie sich im Raum befinden soll.

        plane{y,0 pigment{rgb<1,0,0>}}
        

Mit diesem Befehl erstellen wir eine Ebene, die von x- und z-Achse aufgespannt wird und auf Höhe y=0 verläuft. Besonders schön wirkt der Boden, wenn er nicht einheitlich eine Farbe besitzt, sondern aussieht als wäre er gekachelt. Dazu muss nur etwas am pigment geändert werden:

        plane{y,0 pigment{checker rgb<0,0,0> rgb<1,1,1>}}
        

Dabei werden in diesem Fall die Farben Schwarz und Weiß wie auf einem Schachbrett angeordnet. Damit haben wir nun alle Vorraussetzungen erfüllt um ein nettes Schattenspiel zu erstellen.

Beispiel: Die Bauklötzchen-Burg

Wie am Ende jedes Kapitels wird das erlernte Wissen in einem netten Motiv zusammen gefasst. In unserem Fall machen wir uns daran, eine Bauklötzchen-Burg per Raytracing zu erstellen. Dabei kommen zwei Lichtquellen zum Einsatz, um die Stärke von "POV-Ray(TM)" zu zeigen: Das Erzeugen von realistischen Schatten. Machen wir uns also ans Werk:

        #version 3.6;
        
        camera{ location <-10, 18, -10> look_at <0,0,0> }
        light_source{ <5, 8, -10> color rgb<1,1,1> }
        light_source{ <-5, 8, -10> color rgb<1,1,1> }

        background{rgb<0,0,1>}
        plane{y,0 pigment{checker rgb<0,0,0> rgb<1,1,1>}}

        box{ <0,0,0>,<2,4,2> pigment{rgb<0,1,0>} translate -3.2*x }
        box{ <0,0,0>,<2,4,2> pigment{rgb<1,1,0>} translate 2.9*x }
        box{ <0,0,0>,<2,4,2> pigment{rgb<1,0,0>} scale<1,1.8,0.4> 
        rotate<90,90,0> translate<-3,5,1.8> }
        cylinder{ <0,0,0>,<0,3,0>,1 pigment{rgb<0,0,1>} translate<1,5,1> }
        cone{ <0,0,0>,1.5 <0,2,0>,1e-4 pigment{rgb<1,0,0>} translate<1,8,1> }
        sphere{ <0,0,0>,3 pigment{rgb<1,1,1>} translate<0,3,6> }
        

Bei dem Bild handelt es sich um eine minimalistische Burg aus fünf Bauklötzchen, die einen Schatten auf die Kugel wirft. Als Übung habe ich dabei den exakt gleiche Quader als Grundform genommen und entsprechend verschoben und skaliert. Auch wenn es auf den ersten Blick kompliziert aussieht, ist es oft hilfreich immer die selbe Grundform zu nehmen und sie entsprechend seiner Wünsche anzupassen. So lassen sich die Gegenstände einfacher erstellen.
Um wirklich schöne Schatten zu bekommen, haben wir gleich zwei Lichtquellen definiert. Das ist auch kein Problem, denn beim raytracing können theoretisch beliebig viele Lichtquellen erstellt werden. Problematisch daran ist nur, dass der Rechenaufwand für jede Lichtquelle ansteigt. Somit kann es bei entsprechenden Bildern schon mal ein paar Tage dauern, bis sie fertig erstellt sind. Bei zwei Lichtquellen wie bei unserem Beispiel ist das aber kein Problem. Daher wünsche ich viel Spaß beim erstellen des Beispiels, was dann wie folgt aussehen sollte: